Python机器学习之非线性回归
13 Oct 2017 非线性回归相较于线性回归而言,总带有一丢丢复杂的神秘感。关于线性回归模型相信各位已耳熟能详,因此这里主要讨论非线性回归模型。其实非线性回归中很大一部分是基于多项式的回归模型,即利用曲线方程代替直线方程拟合坐标图上各点,使得各点到曲线的距离总和最短。
一元m次多项式回归方程为:
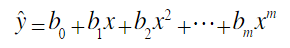
二元二次多项式回归方程为:
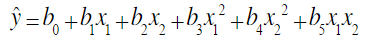
多项式回归的最大优点就是可以通过增加x的高次项对实测点进行逼近,直至满意为止。事实上,多项式回归可以处理很大一类非线性问题,它在分析中占有重要的地位,因为任何一个函数都可以分段用多项式来逼近。
举一个房屋价格与房屋尺寸非线性拟合的实例,数据集下载地址:prices.txt
· 算法构建代码
# python -version 3.5+
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# 读取数据集
datasets_X = [] #建立datasets_X储存房屋尺寸数据
datasets_Y = [] #建立datasets_Y储存房屋成交价格数据
fr = open('E:\\prices.txt', 'r', encoding='utf-8') #指定prices.txt数据集所在路径
lines = fr.readlines() #读取一整个文件夹
for line in lines: #逐行读取,循环遍历所有数据
items = line.strip().split(",") #变量之间按逗号进行分隔
datasets_X.append(int(items[0])) #读取的数据转换为int型
datasets_Y.append(int(items[1]))
# 数据预处理
length = len(datasets_X)
datasets_X = np.array(datasets_X).reshape([length, 1]) #将datasets_X转化为数组
datasets_Y = np.array(datasets_Y)
minX = min(datasets_X) #以数据datasets_X的最大值和最小值为范围,建立等差数列,方便后续画图
maxX = max(datasets_X)
X = np.arange(minX, maxX).reshape([-1, 1])
# 数据建模
poly_reg = PolynomialFeatures(degree=2) #degree=2表示二次多项式
X_poly = poly_reg.fit_transform(datasets_X) #构造datasets_X二次多项式特征X_poly
lin_reg_2 = linear_model.LinearRegression() #创建线性回归模型
lin_reg_2.fit(X_poly, datasets_Y) #使用线性回归模型学习X_poly和datasets_Y之间的映射关系
· 测试结果代码
# 查看回归系数
print('Coefficients:',lin_reg_2.coef_)
# 查看截距项
print('intercept:',lin_reg_2.intercept_)
# 数据可视化
plt.scatter(datasets_X, datasets_Y, color='orange')
plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color='blue')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()
· 部分结果展示
相关系数Coefficients: [ 0.00000000e+00 4.93982848e-02 1.89186822e-05]
截距项intercept: 151.846967505
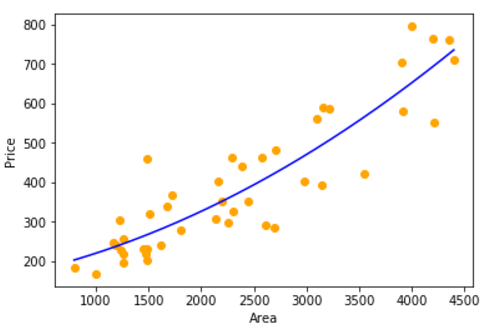
非线性回归公式:Y = 151.8470 + 4.9398e-02*x + 1.8919e-05*x^2
非线性拟合图:
分类: 机器学习算法
