机器学习之模型评估(ROC曲线)
23 Jan 2018模型评估一直是数据建模中不可或缺的一环,评估指标的好坏直接关系到模型上线运用的情况。本文期望以最直观的方式告诉大家模型评估的相关指标,并手动绘制令诸多同学疑惑的ROC曲线。在此希望大家注意:模型评估指标只能作为参考依据,在真正的项目实施过程中,还是需要针对具体业务具体分析。
分类模型(贝叶斯、决策树、SVM等)评估指标:
| 评估指标 | 具体描述 | sklearn对应函数 |
|---|---|---|
| Precision | 精准度 | from sklearn.metrics import precision_score |
| Recall | 召回率 | from sklearn.metrics import recall_score |
| F1 | F1值 | from sklearn.metrics import f1_score |
| Confusion Matrix | 混淆矩阵 | from sklearn.metrics import confusion_matrix |
| ROC | ROC曲线 | from sklearn.metrics import roc |
| AUC | ROC曲线下的面积 | from sklearn.metrics import auc |
回归模型(线性回归、非线性回归等)评估指标:
| 评估指标 | 具体描述 | sklearn对应函数 |
|---|---|---|
| Mean Square Error(MSE/RMSE) | 平均方差 | from sklearn.metrics import mean_squared_error |
| Absolute Error(MAE/RAE) | 绝对误差 | from sklearn.metrics import mean_absolute_error, median_absolute_error |
| R-Squared(R^2) | R平方值 | from sklearn.metrics import r2_score |
· 混淆矩阵、ROC曲线与AUC面积
问题1:混淆矩阵是什么?
回答1:混淆矩阵说简单一点就是预测的正例/反例与真实值之间的比例关系,该矩阵包括4个方面:
| 预测值 | 真实值 | 对应指标 |
|---|---|---|
| 正例 | 正例 | True Positive(TP) |
| 正例 | 反例 | False Positive(FP) |
| 反例 | 正例 | True Negative(TN) |
| 反例 | 反例 | False Negative(FN) |
混淆矩阵图如下:
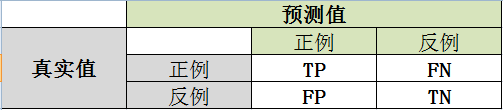
由此计算:
True Positive Rate真实的正例中,被预测正确的比例:TPR = TP/(TP+FN)
False Positive Rate真实的反例中,被预测正确的比例:FPR = FP/(FP+TN)
问题2:混淆矩阵、ROC曲线与AUC面积之间的关系?
回答2:ROC曲线(Receiver Operating Characteristic)主要用于评估二分类模型的优劣,其绘图时X轴和Y轴分别对应混淆矩阵中FPR和TPR,其下方包围的面积为AUC(Area Under the Curve)。
问题3:ROC曲线如何绘制?
回答3:一条曲线的绘制必须是多个点的连线,那么我们就需要在坐标轴上描出多个点,以此来绘制ROC曲线,具体步骤如下:
(1)假设我们有一个100行的数据集,按照9:1划分为训练集和测试集;
(2)接下来我们建立二分类模型并预测结果,这时10行的测试集中每个观测都应该有一个对应的原始分类和预测概率;
| 测试集 | 原始分类 | 预测概率 | 测试集 | 原始分类 | 预测概率 |
|---|---|---|---|---|---|
| 1 | P | 0.9 | 6 | P | 0.49 |
| 2 | P | 0.8 | 7 | N | 0.38 |
| 3 | N | 0.7 | 8 | N | 0.31 |
| 4 | P | 0.6 | 9 | P | 0.3 |
| 5 | P | 0.54 | 10 | N | 0.1 |
(4)这时我们依次将10个预测概率作为阈值threshold,当准确度大于或等于这个值的时候,预测结果为P,否则为N,例如,预测概率值为0.6,那么测试集结果为:
| 测试集 | 原始分类 | 预测分类 | 测试集 | 原始分类 | 预测分类 |
|---|---|---|---|---|---|
| 1 | P | P | 6 | P | N |
| 2 | P | P | 7 | N | N |
| 3 | N | P | 8 | N | N |
| 4 | P | P | 9 | P | N |
| 5 | P | N | 10 | N | N |
由此绘制混淆矩阵:
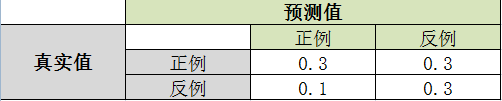
计算TPR与FPR:
TPR = TP/(TP+FN) = 0.3/(0.3+0.3) = 0.5
FPR = FP/(FP+TN) = 0.3/(0.1+0.3) = 0.75
据此,我们每更换一次阈值threshold,就能计算出一组TPR与FPR,那么这个数据集就应该能计算出10组TPR与FPR(其余9组请同学自行推算,不再写出具体计算过程)
(5)由此,我们以FPR为横坐标,TPR为纵坐标,描出所有的坐标点并连线,最终汇出ROC曲线,这里给出ROC曲线样例如下:
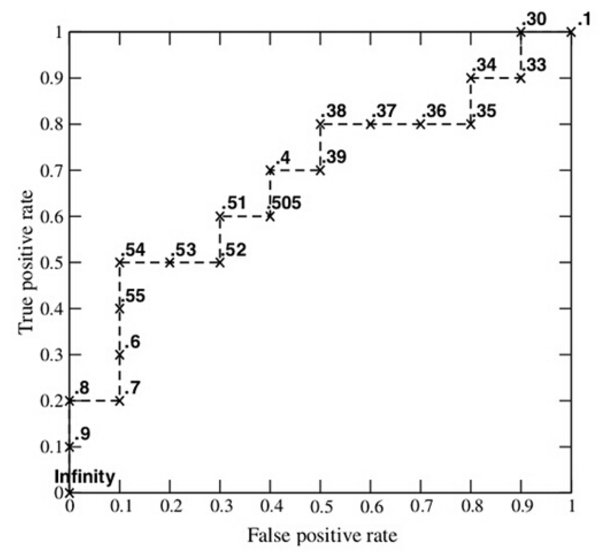
分类: 机器学习算法
