手工计算一个神经网络

  神经网络算法作为深度学习的基础，其重要性不言而喻。然而大部分同学，在实际学习过程中却总不得其门而入。某天受高人指点尝试去手工计算一个三层神经网络，于是一通百通，不仅了解了神经网络工作原理的本质、调优的方法，还用python自写了一套基础版的神经网络算法。本篇博文便一步步的将整个推导过程重现一遍。

1. 了解Sigmoid函数
  Sigmoid函数（简称S函数） 对于大家来说并不陌生，其公式为：y = 1/1+E(-x)。当x趋近无穷大时，y趋近于1；当x趋近无穷小时，y趋近于0。因此S函数的输入x可以为任意数，而输出y必介于0到1之间。
  那么S函数在神经网络中起什么作用呢，大家可以想象一下神经网络是由多个神经元共同作用而成，而神经元的工作方式是在接受输入到达一定量级的时候，才产生相应的输出。因此我们用S函数模拟神经元的工作方式，即当输入x到达一定界值时，S函数（神经元）就激发了。

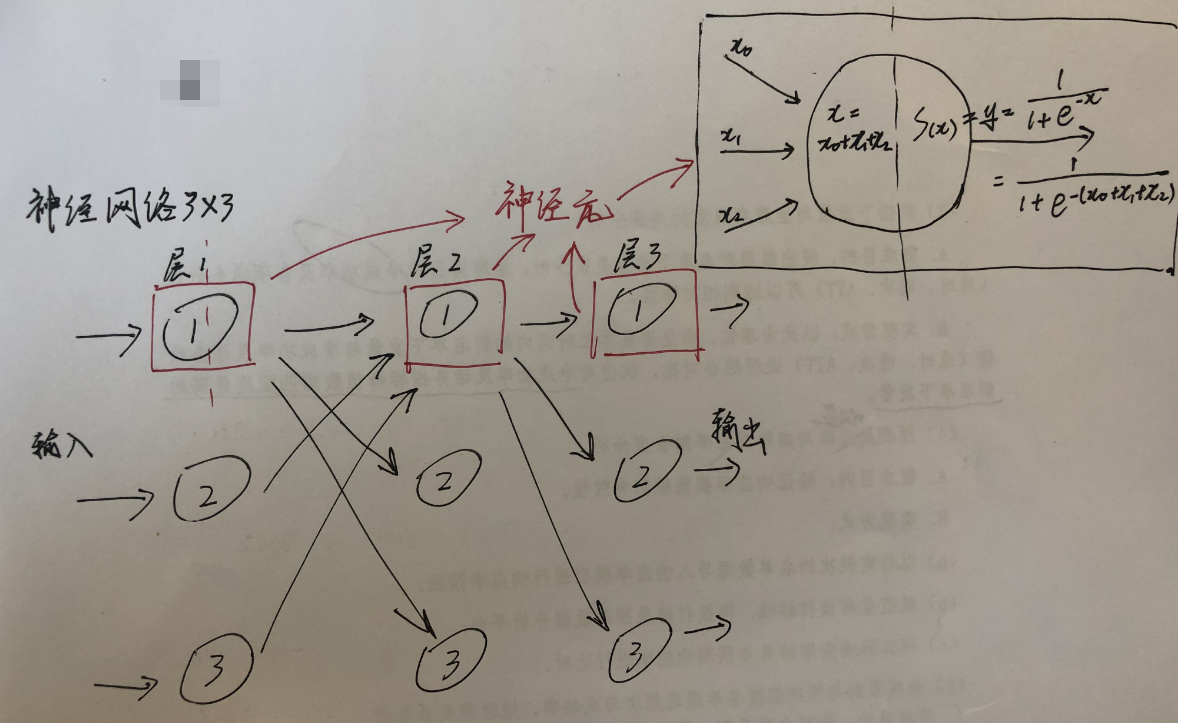
我们举个例子计算一个神经元的输入及输出

例：假设x1=0.05,x2=0.25,x3=0.75求S函数的解         
x = x1+x2+x3 = 0.05+0.25+0.75 = 1.05        
y = 1/1+E(-x) = 1/1+E(-1.05) = 0.7488      

2. 了解W权重
  图1中可以看到，神经网络每个神经元之间都会有连接，而每个连接上都会有相应的权重W，那么神经网络前后层之间为什么要相互连接呢？第一，这种完全连接的方式可以相对容易编辑成计算机指令，第二，神经网络在迭代学习过程中自身会弱化不需要的链接，即权重趋近于0。在这里我们需要注意初始权重是随机值，神经网络需要做的就是不断调整权重以最大降低预测值与真实值之间的误差。加入权重后，单个神经元的计算方式如下图：

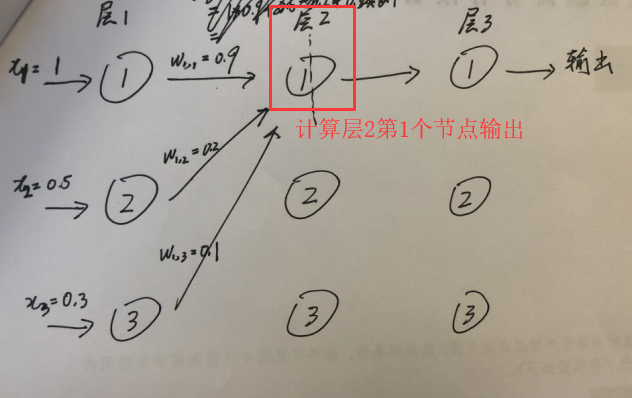
# 第2层第1个神经元输入x        
x = (x1*w1,1)+(x2*w1,2)+(x3*w1,3) = 1*0.9+0.5*0.2+0.5*0.1 = 1.05        
# 第2层第1个神经元输出y   
y = 1/1+E(-x) = 1/1+E(-1.05) = 0.7488      

3. 计算一个三层神经网络
  这里我们先用最基础的方法去计算三层神经网络的输出结果，由于第三层（输出层）每个神经元的计算方式不尽相同，因此我们只计算第三层第一个神经元的输出，如下图：

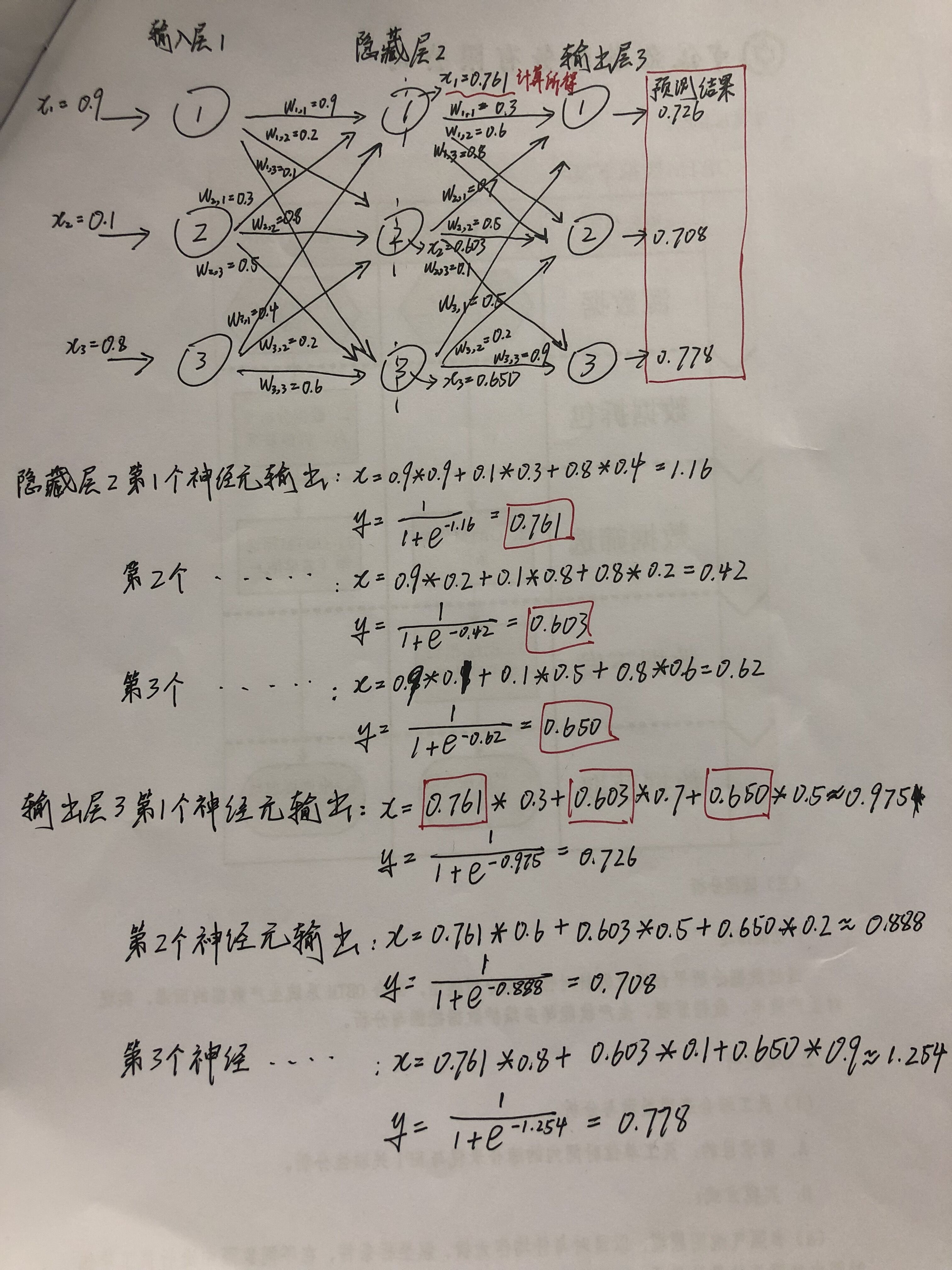
这样我们就成功计算了一个三层神经网络的输出结果，是不是挺容易的？！

4. 借助矩阵计算神经网络
  这里我们借助矩阵的方式去实现3中三层神经网络的计算，如下图：

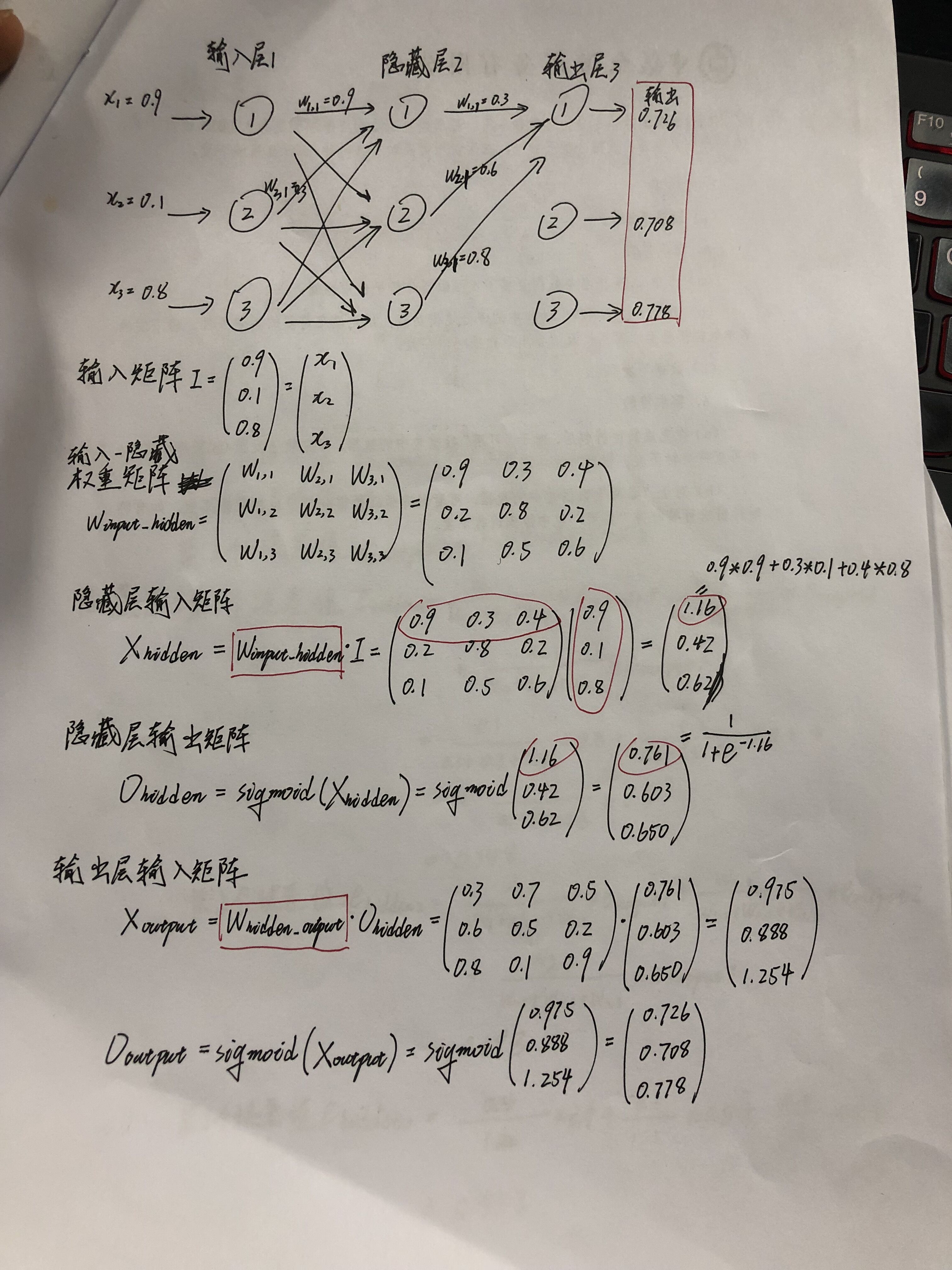
这里我们极大的简化了神经网络的计算方式，并获得了相同的输出结果。后续用Python实现神经网络算法，

5. 如何计算反向传播误差
  误差代表的是我们实际值与预测值之间的差异，即误差e=实际值t-预测值o。在误差反向传播的过程中，我们按照W权重来分配每个神经元的误差，如下图：

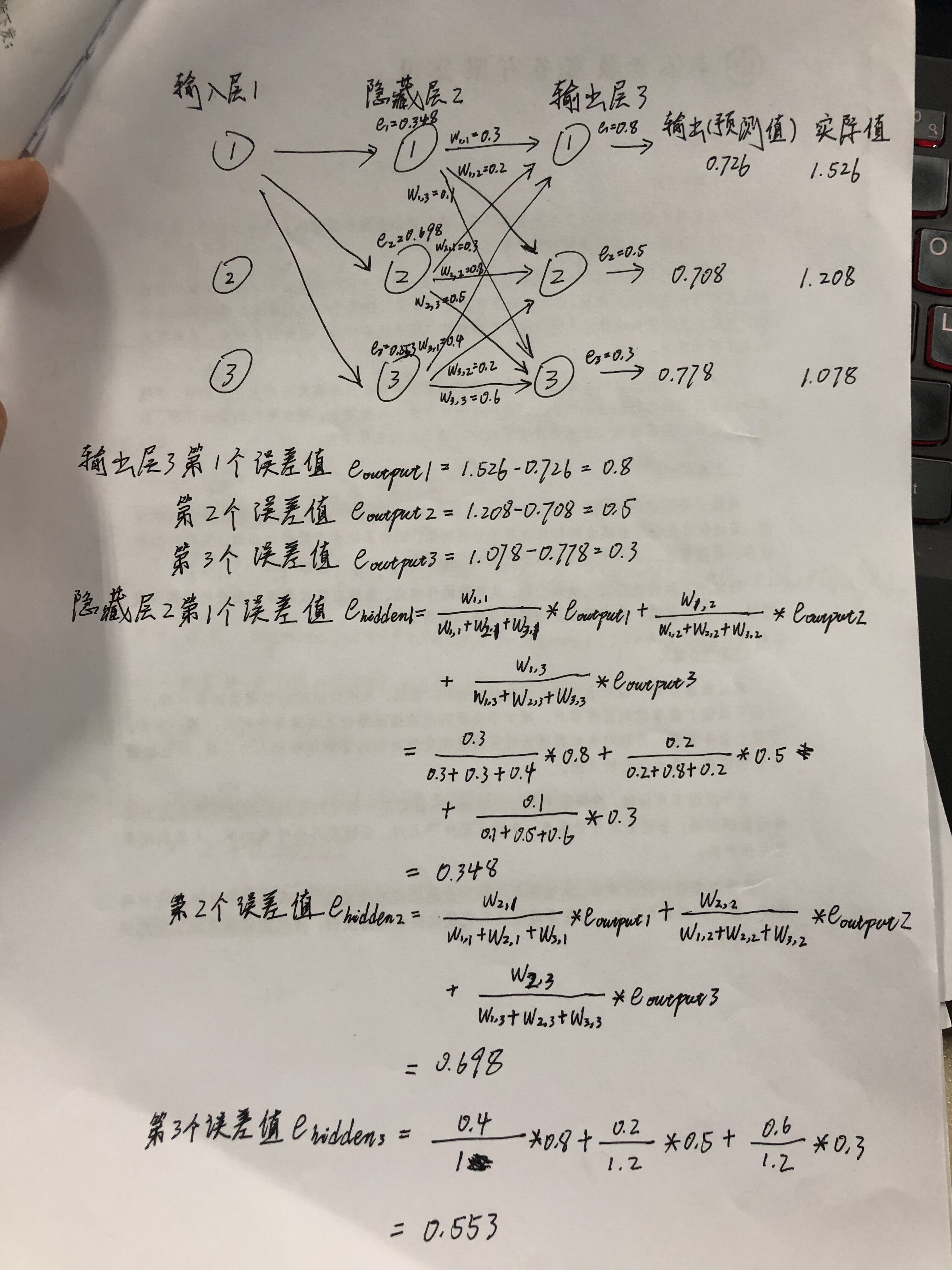
这里我们也可以借助矩阵来计算误差，图中e(hidden)=W(hidden_output)的转置矩阵*e(output)

6. 如何使用误差来调整权重
  计算误差的目的，就是告诉神经网络如何去调整矩阵权重，以使得迭代计算出的预测值不断趋近于真实值。这里直接给出权重计算的公式，如下图：

这样我们整个神经网络的已经计算完成，最后强烈推荐一本书《Python神经网络编程》塔里克·拉希德著，接下来我们再试着用Python来实现一遍。