《数学通识50讲》吴军

· 导论

数学通识教育前提：数学从体系到研究方法，再到应用方法是共通的。
第一模块：数学从猜想=>推论=>实际应用
第二模块：“数的概念”从抽象到具体
第三、四模块：已知几何与代数
第五、六模块：微积分、概率统计
第七模块：数学在其他领域的应用

第七模块
1.数学与哲学：数学如果是最基础的学科，哲学就是最顶头的学科。（一头一尾）
数学对哲学的影响： 笛卡尔《谈谈方法》人是如何获得知识的，人能否通过自身努力获得知识。
靠经验积累有两大问题：一是来的太慢，二是直接经验常常是不可靠的。
解决方法：第一层面是今天所谓的实证，第二层面的理性，就是要用符合逻辑的数学方法去替代测量从而获得真知。
莱布尼茨第一个相对的因果时空观，第二个是离散的世界的理解。
用数学中建立公里化体系的方法，建立自己的哲学体系，就成为了在认知上通用的方法。
哲学对数学的影响：
哲学讲的是宇宙万物的本质，《西方哲学史》罗素
苏格拉底把自己看成主人，就需要在认知层面有所提高，了解数学和哲学都有助于帮助我们做到这一点。
哲学（最顶）=>各种自然科学=>数学（最底） 2.数学与自然科学：一种科学只有在成功运用数学时，才算达到真正完善的地步。（自然科学+数学）
天文学+数学（地心说+几何学）
博物学+数学（分门别类+集合论）
物理学+数学（实验方法+数学方法）
化学+数学（燃素说、氧化说+量化）
自然科学升华过程：
从简单的观察上升到理性的分析
从给出原则性结论到量化的结论
将自然科学公式化
3.数学与逻辑学
同一律：偷换概念、个体换成集合、限量版（所有的商品都是有限的）
矛盾律：不可能即是A又是A
排中律：任何事物，都要有“是”或“非”的判断
充分条件律：因果原理
4.数学与其他学科
运筹学：运用图论、线性代数改进现有系统的效率。
管理学+数学（使命、价值观和文化）
历史学+数学（大历史史书）

· 演讲内容《数学之美》

· 前言

  吴军老师写过一本《数学之美》，其中包括傅里叶级数、马尔科夫假设、自然语言处理方法等，这些数学知识比较专业，很难联系非专业人士的知识，这里期望利用更简单的方法，例如我们会讲到小学数学鸡兔同笼问题讲到初中的等比数列再到大学的线性代数，我们会从数学猜想讲到推论再讲到应用，带领大家感受五大类数学之美。该演讲需要储备以下知识：线性方程组求解、无穷大与无穷小的定义、等比数列计算公式、矩阵乘法。

· 从鸡兔同笼问题开始

  在一个笼子里有鸡和兔子，一共35个头，94只脚，试问鸡和兔子各有几只？

解1：《孙子算经》将所有动物的脚数除以2，一共94/2=47对，每只鸡有一堆脚，兔子有两对脚；假设所有动物都是鸡的话，应该有35对脚，这时需要将鸡换成兔子，47-35=12，说明有12只鸡要换成兔子，兔子数目12，鸡数目23只。
解2：假定笼子里都是鸡，应有35/*2=70条腿，但现在有94条，多出24条，应该是兔子造成的，一只兔子换一只鸡多出2条腿，24/2=12，于是就有12只兔子，其他的都是鸡。
解3：美国小学的教法

兔子的数量	鸡的数量	脚的数量
23	12	116
22	13	114
21	14	112
20	15	110
···	···	···
13	22	96
12	23	94

解4：二元一次方程
设鸡有x只，兔子有y只
x+y=35
2x+4y=94

数学之美：美在针对同一个问题，有多种不同的解法，但即使解法千变万化，正确的答案有且只有一个。

· 毕达哥拉斯定理（勾股定理）

  勾股定理讲的是直角三角形两条直角边的平方之和等于斜边的平方，写出来就是x^2+y^2=z^2。这个定理在国外都被称为毕达哥拉斯定理，接下来有两个疑点：
疑点1.这个定理是否在毕达哥拉斯之前就发现了？
我们过去教科书里，汉朝数学书《周髀算经》记载，早在公元前1000年，周公和商高就两人就谈到了“勾三股四弦五”，比毕达哥拉斯早了500年，于是教科书中认为中国人高商最早提出这个定理，于是被称为勾股定理或高商定理。但如果只是记录了一组勾股数，早在公元前2500年，古埃及人在建造大金字塔时就已经按照勾股数在设计墓室尺寸了，再往前推，美索不达米亚人早在公元前18世纪左右就知道很多勾股数，并留下实物证据。
疑点2.古埃及和美索不达米亚为什么不争夺定理的发现权？
所有这些古代文明不过是举出一些特例而已，甚至没有提出假说，但在数学体系中，光举例是不够的，还需要做出一个明确的规律性的描述，即该定理是需要被证明的而不是例举的，这就是数学与实验科学的不同之处，前者需要依靠严谨的逻辑证明，而后者只需要实验证实就行。
那么勾股定理如何证明呢？

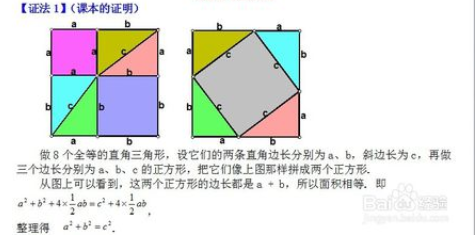
更多证明方法，可参考勾股定理16种证明方法
接下来，我们看看证法1，其中我们要知道直角三角形面积公式和正方形面积公式，再看证法2，我们不仅要知道前者，还需要知道三角形总和为180度，全等三角形角度相等等。

数学之美：美在数学需要经过严格的逻辑推理，公式与公式之间具有强关联性。
既然如此由毕达哥拉斯定理又推理出了什么其他的定理公式么？

· 无理数与黄金分割

  毕达哥拉斯有个很怪的想法，他坚信世界的本源是数字，但数字必须是完美的。整数很完美，而分数的分子分母也都是整数，因此也很完美。整数和分数所构成的有理数让毕达哥拉斯一直坚信自己的想法。
  然而毕达哥拉斯定理被证明以后，就有麻烦了。假设某一直角三角形的两条直角边都是1，那么斜边该是多少呢？根据定理算一下，斜边的平方是2，换句话说就是自己乘以自己等于2的数，这个数是否是完美的有理数呢？
如果它是有理数，那么假定存在一个数字是R，它能够写成R=A/B的形式，数字R^2=2。
由此可以看出需满足3个条件：A、B都是整数，A、B不可再约分（互素），A/B的平方等于2。
从第三个条件出发R^2=A^2/B^2=2，则A^2=2*B^2，这时候A应该是偶数，那么可以写成A=2*C的形式。A^2=4*C^2=2*B^2则2*C^2=B^2，这个时候B也应该是偶数对吧，这下问题来了，A和B都是偶数那不是还可以再约分么？
推导没错，勾股定理没错，我们的认知出了问题。世界上存在一种数，它无法写成有理数的形式，它是无限不循环小数，我们今天把它称为无理数，写成根号2。无理数中有名的除了π，还有黄金分割点1.618（根号5-1除以2）。例如雅典卫城帕特农神庙、断臂的维纳斯、蒙娜丽莎等。
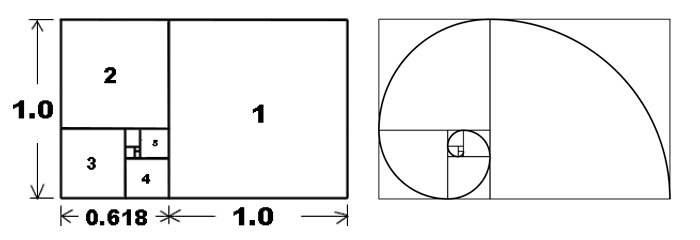
那为什么黄金分割看起来这么顺眼呢？它的美感来自几何图形的相似性。我们拿一个满足黄金比例的长方形，不断减去一个正方形，然后把圆弧连起来，就有了一个等螺线，类似于蜗牛的壳，或者龙卷风的中心点，或者星云图。其实黄金分割反映了宇宙自身的一个常数，人作为宇宙的个体，耳蜗的形状，虹膜纹路都遵循这个常数。因此悦耳的音乐、动人的风景、好看的脸都是符合这个黄金比例的。

优选法中0.618法：
例：钢中加多少碳，馒头中加多少碱，假设每吨加入量在1000克，以1%迭代实验到2000克需要1000次，由此得用0.618黄金分割法。
第一次加入(2000-1000)×0.618+1000=1618克
第二次加入2000-1618+1000=1382克
第三次加入1682-1382+1000=1236克
第四次加入1618-1382+1236=1472克
5次实验可限制在9%以内，6次实验可到6%以内，根据优选法效率可以提高2~3倍。

数学之美：美在它从现实世界中抽象出来再被应用到现实世界中去。

· 数列与级数

  某传销公司提成方式，每个人入会缴纳1万元，发展一个直接下线，从后者身上提成20%，直接下线每发展一个下线，可以从下线身上再提成20%的20%。
问题1：张三入会了，他在什么情况下可挣到钱？
情况1：张三找5个朋友加入这个会，他付出1万元，从每个直接下线获得2000元，类似的每个直接下线再发展5个下线，最终获得共计20000元，赚10000元
情况2：张三找4个朋友加入这个会，他付出1万元，从每个直接下线获得2000元，类似的每个直接线下再发展5个下线，最终获得共计16000元，赚6000元，每少一个直接下线少4000元
情况3：张三找5个朋友加入这个会，他付出1万元，从每个直接下线获得2000元，类似的每个直接下线再发展4个下线，最终获得共计18000元，赚8000元，下线的下线每少一个少2000元
  这是很理想的假设，首先张三得找出3个及以上的朋友，每个朋友又得找到5个及以上的下线，才可能获利400元，但朋友之间有很大的交集，通常张三想发展的人，和他朋友想发展的人是一群人。
问题2：张三如果真的发展了5个人，真能拿到无限多的钱么？
再来看情况1，第一层获得2000*5=1万元，第二层获得400*25=1万元，第三层获得80*125=1万元，第四层获得16*625=1万元，第五层获得3.2*3125=1万元，以此类推
期望获得10万元，需要多少人？
An=a1*q^(n-1)
a1=5
q=5
A10=5*5^9=9765625
总数需要12,207,030人，20万元总数需要119,209,289,550,780。最后后接近无穷大，完全不可能实现。
问题3：那我如果少几个人行不行？
情况4：张三找3个朋友加入这个会，他付出1万元，从每个直接下线获得2000元，类似的每个直接下线再发展3个下线，以此类推
第一层获得2000*3=6000元，第二层获得400*9=3600元，第三层获得80*27=2160元，第四层获得16*81=1296元，第五层获得3.2*243=777.6元，第六层获得0.64*729=466.56元，第七层获得0.128*2187=279.936元，以此类推
级数迅速的收敛，最终无限趋近于1.5万，这便是无穷小的概念。
所以我们在日常理财或者工作中，不能仅仅看到现在的状态，而是看它未来发展的趋势，是发散的还是收敛的，就类似于我们这次的疫情为什么会封城，就是期望将其由发散的趋势迅速转向收敛的趋势，由无穷大转变为无穷小。

数学之美：美在它帮你由静态的感知世界到动态的感知世界，从而看清现实世界中无法看清的问题。

· 线性代数

  回到鸡兔同笼问题，在一个笼子里有鸡和兔子，一共35个头，94只脚，试问鸡和兔子各有几只？
解4：二元一次方程
设鸡有x只，兔子有y只
x+y=35
2x+4y=94
也可写成线性代数形式：
[1 1 35]
[2 4 94]
向量变化
[1 1 35]
[0 2 24]
线性代数中一个很重要的概念便是矩阵，矩阵是一个M行N列，例如上述就是2行3列
假如做资产配置，第一家银行股票基金、债券基金、高风险基金投资回报分别是7%、3%和10%，第二家分别是8%、2%和9%，现在有1万元，你投第一家还是第二家？
矩阵R=([7%,3%,10%],[8%,2%,9%])
假设资产配比P=[3000,2000,5000]
数乘：
7%*3000+3%*2000+10%*1000=650
8%*3000+2%*2000+9%*1000=690 矩阵乘法：
R*P=[650,690]
若是不同的资产配比
P=([3000,2000,5000],[7000,2000,1000],[…])
R*P=([650,690],[770,730],[…])
由此，我们将单个计算变成大批量处理，也是我们今天所处信息时代需要有的思维方式。

数学之美：美在它为你提供一个方便的工具，帮你由单点问题到批量问题的解决。

· 结束语

  我们常常依靠经验和直觉来认识世界，而数学作为一切科学的基础，它化繁为简可以帮助我们思考事物的本质，从而达到一通百通的效果。希望这次演讲能够抛砖引玉，让大家从过去惧怕、讨厌、漠视数学，到理解、喜欢、应用数学，从而感受到真正的数学之美。