数分学长 的博客

HMM隐马尔可夫模型的实例

09 Aug 2017

1.引言

  最近看到许多同学对自然语言处理（NLP）都非常感兴趣，但对于NLP中一些基本的统计模型并不够了解。遂写下该博文，帮助大家掌握NLP中文分词这一大板块比较核心的统计模型——HMM隐马尔可夫模型。
  HMM模型的全称是Hidden Markov Model，看关键词就知道该模型中存在隐含层，它是用来描述一个含有隐含未知参数的马尔可夫过程，其目的是希望通过求解这些隐含的参数来进行实体识别，说简单些也就是起到词语粘合的作用。
  举一个经典的实例：一个北京的朋友每天根据天气【下雨，天晴】决定当天的活动【公园散步,购物,清理房间】中的一种，我每天只能在朋友圈上看到她发的消息 “我前天公园散步，昨天购物，今天清理房间了！”，那么我如何根据她发的消息推断北京这三天的天气？

2.隐马尔可夫模型概述

  任何一个HMM模型都包括如下五方面：
  Obs 显现层
  States 隐含层
  Start_p 初始概率
  Trans_p 转移概率
  Emit_p 发射概率

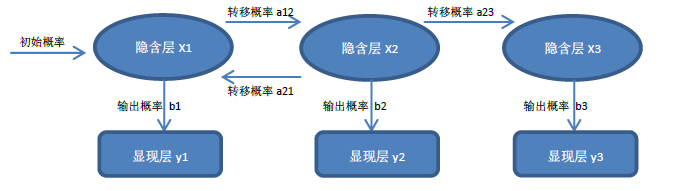图：HMM隐马尔可夫模型变迁图

3.样例计算

命题：“我前天公园散步，昨天购物，今天清理房间了！”

HMM模型的计算公式：

# 隐含层
states = ('Rainy', 'Sunny')
# 显现层
observations = ('walk', 'shop', 'clean')
# 初始概率
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
# 转移概率
transition_probability = {
    'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
}
# 发射概率
emission_probability = {
    'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

【第一天】【散步】= [初始概率,下雨] * [发射概率,散步] = 0.6*0.1 = 0.06
【第一天】【散步】= [初始概率,晴天] * [发射概率,散步] = 0.4*0.6 = 0.24
因为0.24>0.06，所以第一天可能是 晴天

【第二天】【购物】= [初始概率,晴天] * [转移概率,M=>下雨] * [发射概率,购物] = 0.24*0.4*0.4= 0.0384
【第二天】【购物】= [初始概率,晴天] * [转移概率,M=>晴天] * [发射概率,购物] = 0.24*0.6*0.3= 0.0432
【第二天】【购物】= [初始概率,下雨] * [转移概率,M=>下雨] * [发射概率,购物] = 0.06*0.7*0.4= 0.0168
【第二天】【购物】= [初始概率,下雨] * [转移概率,M=>晴天] * [发射概率,购物] = 0.06*0.3*0.3= 0.0054
需要注意的是，这里0.0432是累积概率 ，所以全局最优解： 第一天 晴天；第二天 晴天（不能够理解这句话的同学请继续看第三天）

【第三天】【清理】= [初始概率,晴天,下雨] * [转移概率,M=>下雨] * [发射概率,清理] = 0.0384*0.7*0.5= 0.01344
【第三天】【清理】= [初始概率,晴天,下雨] * [转移概率,M=>晴天] * [发射概率,清理] = 0.0384*0.3*0.1= 0.00115
【第三天】【清理】= [初始概率,晴天,晴天] * [转移概率,M=>下雨] * [发射概率,清理] = 0.0432*0.4*0.5= 0.00864
【第三天】【清理】= [初始概率,晴天,晴天] * [转移概率,M=>晴天] * [发射概率,清理] = 0.0432*0.6*0.1= 0.00259
【第三天】【清理】= [初始概率,下雨,下雨] * [转移概率,M=>下雨] * [发射概率,清理] = 0.0168*0.7*0.5= 0.00588
【第三天】【清理】= [初始概率,下雨,下雨] * [转移概率,M=>晴天] * [发射概率,清理] = 0.0168*0.3*0.1= 0.00050
【第三天】【清理】= [初始概率,下雨,晴天] * [转移概率,M=>下雨] * [发射概率,清理] = 0.0054*0.4*0.5= 0.00108
【第三天】【清理】= [初始概率,下雨,晴天] * [转移概率,M=>晴天] * [发射概率,清理] = 0.0054*0.6*0.1= 0.00032
从这里就能看出，累积概率最大值为0.01344，所以全局最优解：第一天晴天；第二天 下雨；第三天 下雨
注：若认为第二天应该是晴天的同学，请区分全局最优解和局部最优解

Python程序实现

# Python -version 3.5以上版本

# 打印路径概率表
def print_dptable(V):
    print ("    ",)
    for i in range(len(V)):
        print ("%7d" % i,)
    print ()
    for y in V[0].keys():
        print ("%.5s: " % y,)
        for t in range(len(V)):
            print ("%.7s" % ("%f" % V[t][y]),)
        print ()

def viterbi(obs, states, start_p, trans_p, emit_p):
    # 路径概率表 V[时间][隐含层] = 概率
    V = [{}]
    # 中间变量
    path = {}
    # 状态初始化 (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]
    # 对 t > 0 跑一遍维特比算法
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}
        for y in states:
            # 概率 隐含层 =  前状态是y0的初始概率 * y0转移到y的转移概率 * y表现为当前状态的发射概率
            (prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
            # 记录最大概率
            V[t][y] = prob
            # 记录路径
            newpath[y] = path[state] + [y]
        path = newpath
    print_dptable(V)
    (prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
    return (prob, path[state])

# HMM 实例导入
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
    'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
    'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

def example():
    #将实例值传输到viterbi函数
    return viterbi(observations,
                   states,
                   start_probability,
                   transition_probability,
                   emission_probability
                   )
print (example())

Python程序结果

         第1天    第2天   第3天
Rainy:  0.06000 0.03840 0.01344
Sunny:  0.24000 0.04320 0.00259

第3天最大概率值及预测结果：
(0.01344, ['Sunny', 'Rainy', 'Rainy'])

参考文献：
- HMM与分词、词性标注、命名实体识别

分类: 自然语言处理

Related Posts